Shane Chu

Convolutional dictionary learning

So we saw convolutions. Given a filter $\bm d$ and a sparse code $\bm x$, an important insight we saw from the convolution is that the sparse code plays the role of an "indicator", indicating where and how much the filter $\bm d$ should appear in the convolution $\bm d * \bm x$.

Let's leverage this intuition a bit further. What if we have a signal $\bm s$, and that we try to "approximate" $\bm s$ using a sum of convolutions, i.e.,

for which we can visualize as

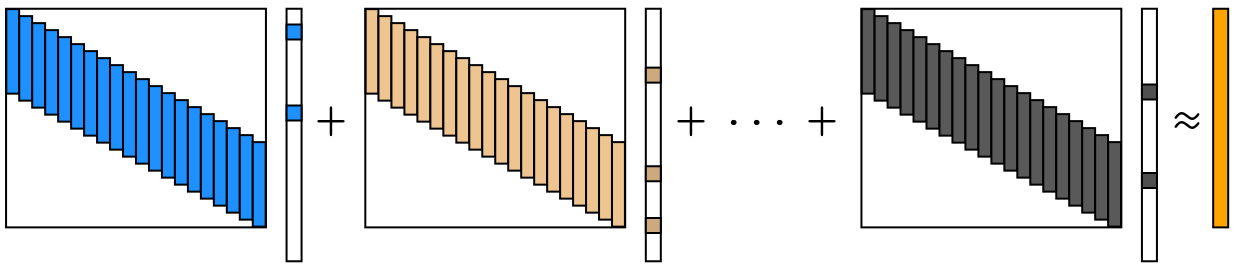
where the orange vector on the right is the signal $\bm s$. Let's formalize this as an optimization problem (single signal case):

i.e., we want to find the best filters $\{\bm d_m\}$ and the sparse code $\{\bm x_m\}$ to represent the signal $\bm s$. The hyperparameter $\lambda$ balances the trade-off between data fitting loss and the sparsity of $\{\bm x_m\}$, and we enforce the constraint $\|\bm d_m\|_2=1$ to avoid the scaling ambiguity in between the filters and the sparse code. We can easily extend this to the case where we have multiple signals:

The problem formulation of (2) and (3) is called a convolutional dictionary learning (CDL) problem. So what's the advantage of formulating the problem as a CDL?

• CDL is highly interpretable:

  In CDL, each signal is approximated by a sparse linear combination of the filters and the sparse code. The sparse code indicates where and how much the filters should appear.

• Minimizing the CDL objective $\Rightarrow$ we obtain specialized filters representing the frequently occurring patterns in the signals.

Equation (1) also shows that CDL is a distributed representation. There's a particular name for this representation: it is a sparse representation — the model uses a sparse linear combination of the filters and the sparse code to describe each signal in the dataset.